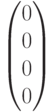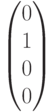Согласно методу декодирования линейного кода по синдрому декодирование осуществляется

Декодирование линейного кода по синдрому
Путь  — матрица размера
— матрица размера  и ранга
и ранга  над полем
над полем 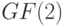 . Эта матрица задает линейное отображение
. Эта матрица задает линейное отображение  пространства
пространства  в пространство
в пространство 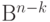 по формуле
по формуле 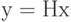 . Ядро этого линейного отображения или множество решений уравнения
. Ядро этого линейного отображения или множество решений уравнения  , образующее подпространство пространства
, образующее подпространство пространства  , является линейным кодом. Можно рассмотреть разбиение пространства
, является линейным кодом. Можно рассмотреть разбиение пространства  на классы равнообразности. В один класс входят все элементы
на классы равнообразности. В один класс входят все элементы  , которые при отображении
, которые при отображении  переходят в один и тот же элемент пространства
переходят в один и тот же элемент пространства 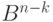 . Элемент пространства
. Элемент пространства 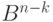 , в который переходят все элементы одного класса, называется синдромом. Pис.7.8 иллюстрирует разбиение пространства
, в который переходят все элементы одного класса, называется синдромом. Pис.7.8 иллюстрирует разбиение пространства  на классы равнообразности.
на классы равнообразности.
Отображение  является отображением на все пространство
является отображением на все пространство 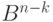 . Для систематической матрицы H это практически очевидно. Действительно, для любого
. Для систематической матрицы H это практически очевидно. Действительно, для любого  можно найти (построить)
можно найти (построить)  , такой, что
, такой, что  .
.
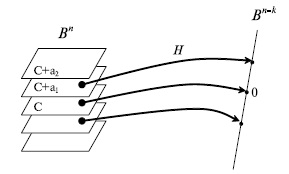
Рис.
7.8.
Разбиение пространства Bn на классы равнообразности
Произведение  называется синдромом [29], [33]. Фактически, синдромом вектора
называется синдромом [29], [33]. Фактически, синдромом вектора 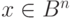 является образ этого вектора при отображении —
является образ этого вектора при отображении — . Все векторы
. Все векторы 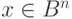 , имеющие один синдром, образуют класс. Так как синдром
, имеющие один синдром, образуют класс. Так как синдром 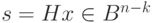 имеет размерность
имеет размерность  , всего существует
, всего существует  классов (если проверочная матрица имеет ранг
классов (если проверочная матрица имеет ранг  , в частности, если матрица
, в частности, если матрица 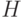 имеет систематический вид). Из определения линейного кода следует, что класс, которому соответствует нулевой синдром, является кодом
имеет систематический вид). Из определения линейного кода следует, что класс, которому соответствует нулевой синдром, является кодом  . Каждый класс
. Каждый класс 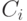 , отличный от кода, порождается «сдвигом»
, отличный от кода, порождается «сдвигом» 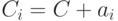 кода
кода  на один из векторов
на один из векторов 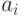 класса
класса 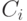 . Действительно, если
. Действительно, если  ., то есть
., то есть  , тогда
, тогда  и, следовательно,
и, следовательно,  и
и 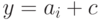 , где
, где 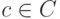 — кодовое слово. Таким образом, любой некодовый вектор, имеющий синдром
— кодовое слово. Таким образом, любой некодовый вектор, имеющий синдром  , можно представить в виде суммы кодового вектора и вектора, имеющего синдром
, можно представить в виде суммы кодового вектора и вектора, имеющего синдром  . Представление такого вида не является единственным. Некодовый вектор
. Представление такого вида не является единственным. Некодовый вектор 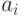 в этой сумме можно рассматривать как вектор ошибок, произошедших в тех разрядах кодового слова
в этой сумме можно рассматривать как вектор ошибок, произошедших в тех разрядах кодового слова  , в которых соответствующие компоненты вектора
, в которых соответствующие компоненты вектора 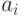 равны 1. Из всех векторов ошибок, имеющих один синдром, наиболее вероятным является вектор
равны 1. Из всех векторов ошибок, имеющих один синдром, наиболее вероятным является вектор 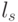 (векторы) с минимальным весом (числом единичных компонент). Такой вектор (векторы) называется лидером класса.
(векторы) с минимальным весом (числом единичных компонент). Такой вектор (векторы) называется лидером класса.
Алгоритм декодирования заключается в следующем. Если получен вектор  и
и  , считаем, что ошибкам соответствует наиболее вероятный вектор из класса
, считаем, что ошибкам соответствует наиболее вероятный вектор из класса  , то есть лидер
, то есть лидер 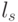 класса
класса  . Тогда декодирование осуществляется в вектор
. Тогда декодирование осуществляется в вектор  , получающийся из принятого вектора удалением лидера.
, получающийся из принятого вектора удалением лидера.
Рассмотрим пример построения кода по заданной проверочной матрице и декодирования полученного сообщения по синдрому. Пусть дана проверочная матрица  . Запишем уравнение для определения кодовых векторов (слов) для данной матрицы:
. Запишем уравнение для определения кодовых векторов (слов) для данной матрицы:

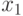 и
и  которые можно рассматривать как информационные разряды, задаются произвольно (всего 4 варианта 00, 01, 10, 11), а проверочные разряды
которые можно рассматривать как информационные разряды, задаются произвольно (всего 4 варианта 00, 01, 10, 11), а проверочные разряды  и
и  определяются через
определяются через 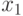 и
и  . В итоге все кодовые слова определяются из выражения
. В итоге все кодовые слова определяются из выражения
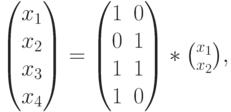
где 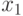 и
и  — информационные разряды, а
— информационные разряды, а  — порождающая матрица, столбцами которой являются кодовые векторы.
— порождающая матрица, столбцами которой являются кодовые векторы.
Кодовые слова, рассматриваемые как векторы-столбцы, образуют матрицу кода

Расстояние кода  равно минимальному весу ненулевого слова
равно минимальному весу ненулевого слова 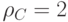 .
.
Найдем смежные классы, которые состоят из векторов пространства 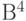 , имеющих одинаковый синдром, и выберем в каждом классе лидера (вектор из класса с минимальным весом).
, имеющих одинаковый синдром, и выберем в каждом классе лидера (вектор из класса с минимальным весом).
Синдромом является любое возможное значение произведения  .
.
В данном случае имеется 4 синдрома:  .Каждому синдрому соответствует смежный класс, синдром
.Каждому синдрому соответствует смежный класс, синдром  соответствует коду. Смежные классы (столбцы матриц) для каждого синдрома и выбранные лидеры приведены в таблице.
соответствует коду. Смежные классы (столбцы матриц) для каждого синдрома и выбранные лидеры приведены в таблице.
В третьем смежном классе — два потенциальных лидера с весом (нормой), равным 1. Один из них выбирается в качестве лидера произвольно.
Рассмотрим на этом примере процесс декодирования полученного вектора (слова) с использованием синдромов. Пусть передавался кодовый вектор  и в процессе переачи произошла ошибка в первом разряде. Это означает, что на приемном конце был получен вектор
и в процессе переачи произошла ошибка в первом разряде. Это означает, что на приемном конце был получен вектор 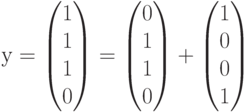 , полученный из переданного вектора
, полученный из переданного вектора  в результате добавления вектора ошибки
в результате добавления вектора ошибки  (ошибка в первом разряде). Определим синдром, вычислив произведение
(ошибка в первом разряде). Определим синдром, вычислив произведение  . В данном случае получим
. В данном случае получим 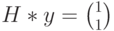 . Это означает, что полученный вектор
. Это означает, что полученный вектор  водит в четвертый смежный класс (см. таблицу). Лидером этого смежного класса является вектор
водит в четвертый смежный класс (см. таблицу). Лидером этого смежного класса является вектор  , соответствующий данному синдрому. Вычитая (добавляя) лидер к принятому вектору, производим декодирование
, соответствующий данному синдрому. Вычитая (добавляя) лидер к принятому вектору, производим декодирование 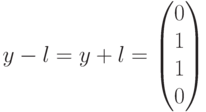 В данном случае декодирование выполнено правильно.
В данном случае декодирование выполнено правильно.
Источник
Путь — матрица размера и ранга над полем . Эта матрица задает линейное отображение пространства в пространство по формуле . Ядро этого линейного отображения или множество решений уравнения , образующее подпространство пространства , является линейным кодом. Можно рассмотреть разбиение пространства на классы равнообразности. В один класс входят все элементы , которые при отображении переходят в один и тот же элемент пространства . Элемент пространства , в который переходят все элементы одного класса, называется синдромом. Pис.7.8 иллюстрирует разбиение пространства на классы равнообразности.
Отображение является отображением на все пространство . Для систематической матрицы H это практически очевидно. Действительно, для любого можно найти (построить) , такой, что .
Рис. 7.8.Разбиение пространства Bn на классы равнообразности
Произведение называется синдромом [29], [33]. Фактически, синдромом вектора является образ этого вектора при отображении -. Все векторы , имеющие один синдром, образуют класс. Так как синдром имеет размерность , всего существует классов (если проверочная матрица имеет ранг , в частности, если матрица имеет систематический вид). Из определения линейного кода следует, что класс, которому соответствует нулевой синдром, является кодом . Каждый класс , отличный от кода, порождается «сдвигом» кода на один из векторов класса . Действительно, если ., то есть , тогда и, следовательно, и , где — кодовое слово. Таким образом, любой некодовый вектор, имеющий синдром , можно представить в виде суммы кодового вектора и вектора, имеющего синдром . Представление такого вида не является единственным. Некодовый вектор в этой сумме можно рассматривать как вектор ошибок, произошедших в тех разрядах кодового слова , в которых соответствующие компоненты вектора равны 1. Из всех векторов ошибок, имеющих один синдром, наиболее вероятным является вектор (векторы) с минимальным весом (числом единичных компонент). Такой вектор (векторы) называется лидером класса.
Алгоритм декодирования заключается в следующем. Если получен вектор и , считаем, что ошибкам соответствует наиболее вероятный вектор из класса , то есть лидер класса . Тогда декодирование осуществляется в вектор , получающийся из принятого вектора удалением лидера.
Рассмотрим пример построения кода по заданной проверочной матрице и декодирования полученного сообщения по синдрому. Пусть дана проверочная матрица . Запишем уравнение для определения кодовых векторов (слов) для данной матрицы:
и которые можно рассматривать как информационные разряды, задаются произвольно (всего 4 варианта 00, 01, 10, 11), а проверочные разряды и определяются через и . В итоге все кодовые слова определяются из выражения
где и — информационные разряды, а — порождающая матрица, столбцами которой являются кодовые векторы.
Кодовые слова, рассматриваемые как векторы-столбцы, образуют матрицу кода
Расстояние кода равно минимальному весу ненулевого слова .
Найдем смежные классы, которые состоят из векторов пространства , имеющих одинаковый синдром, и выберем в каждом классе лидера (вектор из класса с минимальным весом).
Синдромом является любое возможное значение произведения .
В данном случае имеется 4 синдрома: .Каждому синдрому соответствует смежный класс, синдром соответствует коду. Смежные классы (столбцы матриц) для каждого синдрома и выбранные лидеры приведены в таблице.
В третьем смежном классе — два потенциальных лидера с весом (нормой), равным 1. Один из них выбирается в качестве лидера произвольно.
Рассмотрим на этом примере процесс декодирования полученного вектора (слова) с использованием синдромов. Пусть передавался кодовый вектор и в процессе переачи произошла ошибка в первом разряде. Это означает, что на приемном конце был получен вектор , полученный из переданного вектора в результате добавления вектора ошибки (ошибка в первом разряде). Определим синдром, вычислив произведение . В данном случае получим . Это означает, что полученный вектор водит в четвертый смежный класс (см. таблицу). Лидером этого смежного класса является вектор , соответствующий данному синдрому. Вычитая (добавляя) лидер к принятому вектору, производим декодирование В данном случае декодирование выполнено правильно.
Лекция 8
Процессам обработки, в том числе и обработке данных, присуще свойство, заключающееся в том, что обработка состоит из нескольких стадий, этапов, операций, которые могут рассматриваться как более простые процессы (подпроцессы) обработки. Стадии обработки могут быть взаимосвязаны. Выполнение тех или иных этапов обработки зависит от результатов выполнения других этапов.
Описание процессов обработки осуществляется в виде совокупности предписаний или достаточно простых действий, которые должны быть выполнены для придания объекту обработки желаемых свойств. Подобные описания, представленные в формализованном виде, обычно называются алгоритмами.
Для исследования процессов обработки данных используются различные формальные модели: конечные автоматы, сети Петри, взаимодействующие последовательные процессы Хоара, системы и сети массового обслуживания и многие другие. Они описывают различные аспекты процессов обработки. Некоторые из этих моделей рассматриваются далее.
Источник
Слово «синдром» означает обычно совокупность признаков, характерных для того или иного явления. Такой же примерно смысл имеет понятие «синдром» и в теории кодирования. Синдром вектора, содержащего, быть может, ошибки, дает возможность распознать наиболее вероятный характер этих ошибок. Правда, определение, которое мы приводим ниже, не сразу позволяет это увидеть. Синдромом вектора и называется вектор s(u), определяемый равенством:
s(u) = uHT.
Из правила перемножения матриц следует, что синдром есть вектор длины m, где m — число строк проверочной матрицы. В силу определения синдрома вектор u тогда и только тогда является кодовым (u ∈ V) когда его синдром равен нулевому вектору. В самом деле, равенство
uHТ = 0
равносильно тому, что координаты х1, х2, …, хn вектора u удовлетворяют проверочным соотношениям (1) из § 11.
Пусть теперь вектор u не является кодовым, тогда этот вектор обязательно содержит ошибочные символы. Вектор и можно представить тогда в виде суммы посланного кодового вектора υ (который пока не известен) и вектора ошибки е:
u = υ + е. (1)
Ясно, что вектор е = (ε1, ε2, …, εn) содержит ненулевые символы в тех позициях, в которых вектор u содержит искаженные символы.
Важным обстоятельством является то, что синдромы принятого вектора u и вектора ошибки совпадают. Действительно,
s(u) = (υ + е) HT = υHT + еHT = еНТ = s(e). (2)
Рассмотрим теперь множество U всех векторов u’, имеющих тот же синдром, что и вектор u. Пусть а = u’ — u. Тогда
s(a) = (u’ — u)HT = u’HT — uHT = s(u’) — s(u) = 0.
Так как s(a) = 0, то а — кодовый вектор. Обратно, если u’-u — кодовый вектор, то s(u’) = s(u). Таким образом, для интересующего нас множества U имеем:
U = {u + a | a ∈ V}.
На языке теории групп это означает, что U есть смежный класс по подгруппе V (пространство Ln и его кодовое подпространство V можно рассматривать соответственно как группу и ее подгруппу относительно операции сложения векторов).
Сказанное позволяет сделать следующие выводы:
1. Два вектора имеют одинаковый синдром тогда и только тогда, когда они принадлежат одному смежному классу по кодовому подпространству. Таким образом, синдром вектора однозначно определяет тот смежный класс, которому этот вектор принадлежит.
2. Вектор ошибки e для вектора u нужно искать в силу равенства (2) в том же смежном классе, которому принадлежит и сам вектор u.
Разумеется, указание смежного класса, которому принадлежит вектор e, еще не определяет самого этого вектора. Естественно выбрать в качестве в тот вектор смежного класса, для которого вероятность совпадения с е наибольшая. Такой вектор называют лидером смежного класса. Если предположить, что большее число ошибок совершается с меньшей вероятностью, то в качестве лидера следует взять вектор наименьшего веса данного класса и в дальнейшем лидер будет пониматься именно в этом смысле.
При реализации алгоритма декодирования по синдрому составляют таблицу, в которой указываются синдромы si и лидеры ei соответствующих им смежных классов. Алгоритм декодирования заключается тогда в следующем:
1. Вычисляем синдром s(u) принятого вектора u.
2. По синдрому s(u) = si определяем из таблицы лидер ei соответствующего смежного класса.
3. Определяем посланный кодовый вектор υ как разность
υ = u — ei.
Может случиться, что в некоторых смежных классах окажется более одного лидера. Если искаженный вектор u попал в один из таких смежных классов, то разумнее отказаться от исправления ошибки, ограничившись ее обнаружением.
При всей своей простоте и прозрачности алгоритм синдромного декодирования обладает серьезным недостатком. Заключается он в том, что устройство, реализующее этот способ декодирования, должно хранить информацию о лидерах и синдромах. Объем же этой информации может оказаться очень большим даже при умеренных длинах кодовых слов (порядка нескольких десятков). В этом нетрудно убедиться — ведь число лидеров и синдромов совпадает с числом смежных классов, которое по теореме Лагранжа равно qn : qk = qn-k. Так что, например, для двоичного (50, 40)-кода получится 1024 лидеров и столько же синдромов, а для (50,30)-кода число их превзойдет миллион.
Таким образом, мы либо придем к чрезмерному усложнению аппаратуры для синдромного декодирования, либо практически вообще не сможем ее построить. К счастью, имеются коды, декодирование которых не требует обращения к таблице лидеров и синдромов. Простейшие из них — это код Хемминга и его расширенный вариант, рассмотренные в § 9.
Как мы уже знаем, двоичный код Хемминга является линейным, в общем случае имеет длину n = 2m — 1, исправляет одиночные ошибки и обходится минимально возможным для этой цели числом проверок (это число равно m). Таким образом, проверочная матрица кода Хемминга имеет порядок m × (2m — 1). При этом все столбцы этой матрицы должны быть ненулевыми и различными (см. § 11, задача 5). Каждый столбец есть двоичный вектор длины m; всего имеется 2m таких векторов, поэтому для построения проверочной матрицы кода Хемминга длины 2m — 1 нужно выписать (в качестве столбцов этой матрицы) все ненулевые двоичные векторы длины m. Порядок столбцов безразличен, но чаще всего их упорядочивают так, чтобы содержимое каждого столбца являлось двоичной записью его номера (сравни с матрицей (2) из § 11). Вот как выглядит проверочная матрица кода Хемминга длины 15 (m = 4):

Алгоритм исправления одиночных ошибок в этом случае удивительно прост. Если вектор и содержит ошибочный символ в i-й позиции, то синдром s(u) этого вектора совпадает с i-м столбцом проверочной матрицы. Таким образом, этот синдром, читаемый как двоичное число, и есть номер ошибочного символа.
Код Хемминга и в общем случае допускает усовершенствование того же рода, что и (7,4)-код из § 9. Добавление проверочного символа α0, осуществляющего общую проверку на четность, приводит, как и там, к расширенному коду Хемминга с дополнительной способностью обнаруживать Двойные ошибки. Его проверочная матрица легко может быть получена из матрицы кода Хемминга: к каждой строке последней следует впереди приписать нулевой символ, а к получившимся строкам — строку из единиц, соответствующую общей проверке на четность:
α0 + α1 + α2 + … + αn = 0.
Например, из приведенной выше проверочной матрицы для (15,11)-кода Хемминга получается следующая проверочная матрица для расширенного (16,11)-кода:

При вычислении синдрома искаженного вектора возможны две основные ситуации: либо синдром совпадает с одним из столбцов проверочной матрицы, либо это не так. Читатель легко проверит, что первая ситуация соответствует нечетному числу ошибок в слове, а вторая — четному.
В первом случае считаем, что произошла одиночная ошибка, и ее положение определяется номером столбца, с которым совпадает синдром.
Во втором случае считаем, что допущены две или любое большее четное число ошибок, если s(u) ≠ 0. Если же s(u) = 0, то, как обычно, полагаем, что ошибок при передаче не было.
Источник
Путь ![]() —матрица размера
—матрица размера ![]() и
и
ранга![]() над
над
полем![]() .
.
Этаматрица задает
линейное отображение ![]() пространства
пространства![]() впространство
впространство ![]() по формуле
по формуле ![]() .Ядро этого
.Ядро этого
линейного отображения или множество
решений уравнения ![]() ,
,
образующее подпространство пространства![]() ,
,
являетсялинейным
кодом.
Можно рассмотреть разбиение пространства ![]() на
на
классы равнообразности. В одинкласс входят
все элементы ![]() ,
,
которые при отображении![]() переходят
переходят
в один и тот же элемент пространства![]() .
.
Элемент пространства![]() ,
,
в который переходят все элементы одного
класса, называется
синдромом.Pис.7.8 иллюстрирует разбиение пространства ![]() на
на
классы равнообразности.
Отображение ![]() является
является
отображением на всепространство ![]() .
.
Для систематической матрицы H это
практически очевидно. Действительно,
для любого![]() можно
можно
найти (построить)![]() ,
,
такой, что![]() .
.

Рис.
7.8. Разбиение
пространства Bn на классы равнообразности
Произведение ![]() называется
называется
синдромом[29], [33].
Фактически, синдромом вектора ![]() является
является
образ этого вектора при отображении
—![]() .
.
Все векторы![]() ,
,
имеющие один синдром, образуюткласс.
Так как синдром ![]() имеетразмерность
имеетразмерность ![]() ,
,
всего существует![]() классов
классов
(если проверочнаяматрица имеетранг ![]() ,
,
в частности, еслиматрица ![]() имеетсистематический вид).
имеетсистематический вид).
Из определения линейного кода следует,
что класс,
которому соответствует нулевой синдром,
является кодом ![]() .
.
Каждыйкласс ![]() ,
,
отличный от кода, порождается
«сдвигом»![]() кода
кода![]() на
на
один из векторов![]() класса
класса![]() .
.
Действительно, если![]() .,
.,
то есть![]() ,
,
тогда![]() и,
и,
следовательно,![]() и
и![]() ,
,
где![]() —
—
кодовоеслово.
Таким образом, любой некодовый вектор,
имеющий синдром ![]() ,
,
можно представить в виде суммы кодового
вектора и вектора, имеющего
синдром![]() .Представление такого
.Представление такого
вида не является единственным.
Некодовый вектор ![]() в
в
этой сумме можно рассматривать
каквектор ошибок,
произошедших в тех разрядах кодового
слова ![]() ,
,
в которых соответствующие компоненты
вектора![]() равны
равны
1. Из всех векторов ошибок, имеющих один
синдром, наиболее вероятным
являетсявектор ![]() (векторы)
(векторы)
с минимальным весом (числом
единичныхкомпонент).
Такой вектор (векторы)
называется лидером класса.
Алгоритм декодирования
заключается в следующем. Если
получен вектор ![]() и
и![]() ,
,
считаем, что ошибкам соответствует
наиболее вероятныйвектор из
класса ![]() ,
,
то есть лидер![]() класса
класса![]() .
.
Тогдадекодирование осуществляется
ввектор ![]() ,
,
получающийся из принятого вектора
удалением лидера.
Рассмотрим
пример построения кода по заданной
проверочной матрице и декодирования
полученного сообщения по синдрому.
Пусть дана проверочная матрица  .
.
Запишем уравнение для определения
кодовых векторов (слов) для данной
матрицы:
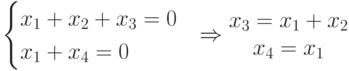
![]() и
и ![]() которые
которые
можно рассматривать как информационные
разряды, задаются произвольно (всего 4
варианта 00, 01, 10, 11), а проверочные
разряды![]() и
и![]() определяются
определяются
через![]() и
и![]() .
.
В итоге все кодовые слова определяются
из выражения

где ![]() и
и![]() —
—
информационные разряды, а —
—
порождающаяматрица,
столбцами которой являются кодовые
векторы.
Кодовые
слова, рассматриваемые как векторы-столбцы,
образуют матрицу кода

Расстояние кода ![]() равно
равно
минимальному весу ненулевого слова![]() .
.
Найдем
смежные классы, которые состоят из
векторов пространства ![]() ,
,
имеющих одинаковый синдром, и выберем
в каждом классе лидера (вектор из
класса с минимальным весом).
Синдромом
является любое возможное значение произведения ![]() .
.
В
данном случае имеется 4 синдрома: ![]() .Каждому
.Каждому
синдрому соответствует смежныйкласс,
синдром ![]() соответствует
соответствует
коду. Смежные классы (столбцы матриц)
для каждого синдрома и выбранные лидеры
приведены в таблице.
Синдром |
|
|
|
|
Класс |
|
|
|
|
Лидер |
|
|
|
|
В
третьем смежном классе — два потенциальных
лидера с весом (нормой), равным 1. Один
из них выбирается в качестве лидера
произвольно.
Рассмотрим
на этом примере процесс декодирования
полученного вектора (слова) с использованием
синдромов. Пусть передавался
кодовый вектор  и
и
в процессе переачи произошла ошибка в
первом разряде. Это означает, что на
приемном конце был полученвектор  ,
,
полученный из переданного вектора в
в
результате добавления вектора
ошибки (ошибка
(ошибка
в первом разряде). Определим синдром,
вычисливпроизведение ![]() .
.
В данном случае получим![]() .
.
Это означает, что полученныйвектор ![]() водит
водит
в четвертый смежныйкласс (см.
таблицу). Лидером этого смежного класса
является вектор  ,
,
соответствующий данному синдрому.
Вычитая (добавляя) лидер к принятому
вектору, производимдекодирование 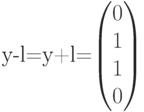 В
В
данном случаедекодирование выполнено
правильно.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник