Синдром ошибки в циклическом коде
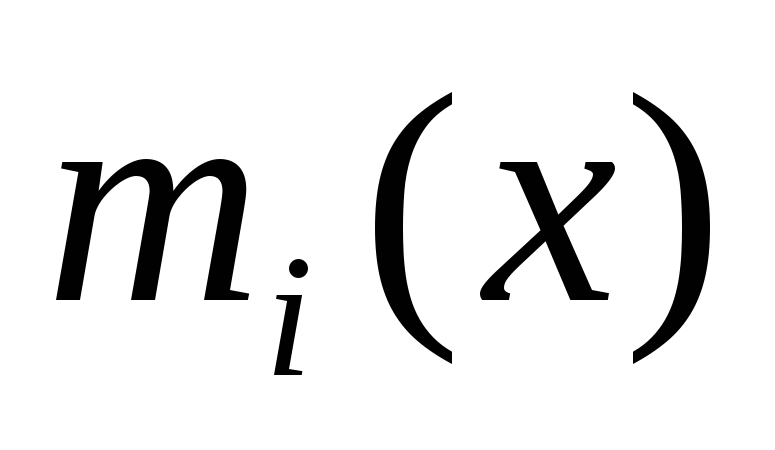
6. Исправление ошибок с помощью циклических кодов
В разделе 3 было показано, что для декодирования правильно принятого кодового слова, т. е. нахождения соответствующего информационного слова, достаточно многочлен, соответствующий принятому кодовому слову, разделить на порождающий многочлен кода. Однако если при передаче произошли ошибки, то в процессе декодирования необходимо эти ошибки исправить.
Поскольку циклические коды являются линейными, то процесс обнаружения и исправления ошибок связан с нахождением синдрома принятого вектора. Напомним, что синдром вектора uвычисляется как произведение вектора на транспонированную проверочную матрицу кода, т. е. su= uHT. В случае циклического кода синдром равен остатку от деления соответствующего многочлена на порождающий многочлен кода, если проверочная матрица строится определенным образом. Иными словами, если g(x) — порождающий многочлен кода, то синдром вектора u равен остатку от деления u(x) на g(x). Если ошибок не было, то остаток, а следовательно, и синдром принятого вектора, равен 0.
Для того чтобы произвести исправление ошибок нам необходимо построить таблицу, в которой в одном столбце будут все возможные векторы ошибок, которые данный код может исправить, а во втором столбце — соответствующие им синдромы. Исправление ошибок, общее для всех линейных кодов, будет следующим:
1. Для принятого слова находим синдром многочлена, соответствующего принятому слову.
2. Если синдром не равен 0, то по полученному синдрому (остатку от деления) находим в таблице соответствующий ему вектор ошибок.
3. Исправляем принятое слово путем сложения по модулю 2 с вычисленным вектором ошибок.
Первый шаг, который выполняется умножением принятого слова на транспонированную проверочную матрицу, для циклических кодов очень простой, если матрица H является проверочной матрицей систематического кода. В этом случае, j-я строка транспонированной матрицы HT соответствует остатку от деления многочлена xn-1-j на порождающий многочлен кода, и синдром равен остатку от деления многочлена, соответствующего принятому слову, на порождающий многочлен кода.
Пример: Рассмотрим циклический (7,1)-код, порожденный многочленом g(x) = x6 +x5 +x4 +x3 + x2 +x +1. Код состоит из двух слов 0000000 и 1111111 и исправляет все комбинации из 3 или менее ошибок. Образующими являются все булевы векторы длины 7 веса 0, 1, 2 и 3. Проверочная матрица строится по частному (x +1) от деления x7 +1 на x6 +x5 +x4 +x3 + x2 +x +1 и имеет вид
Пусть принято слово 11101101, которое соответствует многочлену x6 +x5 +x4 + x2 + 1. Остаток от деления этого многочлена на порождающий многочлен кода равен x3 + x. Непосредственной проверкой можно убедиться, что при умножении вектора u = 1110101 на транспонированную матрицу HT, так же как и при умножении вектора 0001010 на HT получается вектор 0001010, который соответствует многочлену x3 + x. Вектор, соответствующий многочлену x3 + x, имеет вес 2, т. е. является образующим смежного класса. Сложив принятый вектор 11101101 с образующим 0001010, мы получим кодовое слово 1111111, т. е. ошибка будет исправлена.
Для линейных кодов число различных синдромов равно 2n—k, где n—k — число проверочных символов. Поэтому для кодов с большой длиной кодового слова, т. е. с достаточно большим числом проверочных символов, таблица синдромов получается очень большая, и потребуется много времени на поиск вектора ошибок. Для уменьшения количества строк в этой таблице для циклических кодов можно воспользоваться строгой математической структурой таких кодов. Основной теоремой является теорема Мегитта, которая устанавливает связь между циклическими сдвигами вектора и их остатками от деления на порождающий многочлен кода.
Теорема 6.1. (Меггит). Пусть s — синдром вектора u длины n. Синдром циклического сдвига вектора u совпадает с синдромом вектора, соответствующего полиному xs(x).
Пример: Рассмотрим (7,4)-код Хэмминга, который является циклическим кодом, порожденным многочленом g(x) = x3 + x+ 1. двоичный вектор 1011000 является кодовым словом, так как соответствующий многочлен x6 + x4 + x3 делится на g(x). Предположим, что при передаче этого кодового слова произошла одна ошибка в разряде, соответствующем x4, и принято слово u = 1001000. Синдром s принятого вектора равен 110, что соответствует многочлену x2 + x.
Рассмотрим циклический сдвиг 0010001 вектора u. Ему соответствует многочлен x4 + 1. Непосредственной проверкой можно убедиться, что остаток от деления многочленаx4 + 1 на многочлен x3 + x+ 1 равен x2 + x+ 1, т. е. синдром вектора 0010001 равен 111. Остаток от деления полинома xs(x) = x3 + x2 на x3 + x+ 1 также равен x2 + x+ 1.
Используя теорему Мегитта, в таблице синдромов можно хранить только синдромы векторов ошибок, соответствующие ошибкам в старшем разряде. Процедура исправления ошибок содержит следующие шаги:
1. Находим синдром принятого вектора, разделив соответствующий многочлен на порождающий многочлен кода. Если остаток от деления, содержащийся в регистре равен 0, то ошибок не было, и частное от деления есть искомое информационное слово. Иначе сравниваем остаток от деления со всеми синдромами, содержащимися в таблице.
2. Если остаток совпал с одним из синдромов таблицы, то прибавляем соответствующий вектор ошибок к принятому слову, делим полученное слово на порождающий многочлен кода; частное от деления есть искомое информационное слово. Если остаток xs(x) не совпадает ни с одним из синдромов таблицы, умножаем s(x) наx и делим многочлен xs(x) на порождающий многочлен кода.
3. Выполняем Шаг 2 до тех пор, пока после p шагов остаток не совпадет с одним из синдромов таблицы. После этого циклически сдвигаем соответствующий вектор ошибок p раз, прибавляем полученный вектор к принятому слову, делим полученное слово на порождающий многочлен кода; частное от деления есть искомое информационное слово.
Пример: Рассмотрим циклический (7,4)-код Хэмминга, порожденным многочленом g(x) = x3 + x+ 1. Соответствующая таблица декодирования с синдромами имеет следующий вид.
Образущий | Синдром |
0000000 | 000 |
Данный код исправляет одну ошибку. Чтобы проиллюстрировать работу декодера Мегитта, оставим в таблице один класс
Образущий | Синдром |
1000000 | 101 |
и предположим, что в переданном кодовом слове 0001011 произошла одна ошибка, т. е. принято, например, слово 0101011, которому соответствует многочлен x5 + x3 + x+ 1. Остаток от деления многочлена x5 + x3 + x+ 1 на порождающий многочлен кода g(x) = x3 + x+ 1 равен x2 + x+ 1, т. е. синдром принятого вектора отличен от 0 и равен 111. Такого синдрома в таблице нет, и следовательно, в старшем разряде ошибок нет. Умножаем многочлен x2 + x + 1, соответствующий синдрому 111, на x и делим полученный многочлен x3 + x2 + xна g(x). Остаток от деления многочлена x3 + x2 + x на x3 + x+ 1 равен x2 + 1, т. е. синдром 101, соответствующий остатку, совпадает с синдромом в сокращенной таблице декодирования. Соответственно, образующий 100000 смежного класса сдвигается на один разряд влево, и полученный вектор 0100000 складывается с принятым вектором 0101011. В результате получается слово 0001011, которое и является переданным кодовым словом, т. е. ошибка будет исправлена.
Можно упростить этот декодер. В частности, при циклическом сдвиге принятого слова многие из исправляемых конфигураций ошибок могут появиться несколько раз. Если удалить один из этих синдромов, то при соответствующем циклическом сдвиге ошибка все-таки будет найдена. Следовательно, для каждой такой пары достаточно запоминать только один синдром.
Источник
Циклический
код
является разновидностью помехоустойчивых
кодов, применяется в технике передачи
дискретных сообщений. Особенности
циклических кодов заключены в двух
свойствах разрешенных кодовых комбинаций:
1. любая
из разрешенных кодовых комбинаций
циклического кода делится по модулю
два без остатка на некоторое, так
называемое «образующее двоичное число»,
определяющее помехоустойчивые свойства
кода, т.е. расстояние d![]() ;
;
2.
циклический сдвиг разрядов разрешенной
кодовой комбинации на один элемент
влево порождает другую разрешенную
кодовую комбинацию.
Например:
01011 и 10110 – две разрешенные кодовые
комбинации некоторого циклического
кода с образующим числом 1011 (d![]() =3).
=3).
Поэтому они делятся по модулю два без
остатка на образующее число:



 1011
1011
1011 10110 1011
0000
01
1011
10
1011
0000
1011
0000
000
000
При
этом d![]() =4
=4
>d![]() =3.
=3.
Кроме
того циклический сдвиг на один разряд
влево элементов первой комбинации
порождают вторую комбинацию.

01011 => 10110
Делимость
без остатка разрешенных кодовых
комбинаций на известное образующее
число лежит в основе операций обнаружения
и исправления ошибок при использовании
циклических кодов.
Структурная
схема СПДС, содержит кодер и декодер
циклического кода. Структура разрешенных
кодовых комбинаций циклического кода
состоит из двух частей. В начале комбинации
располагается n-проверочных
разрядов, структура которых определяется
кодерами циклического кода из условия
обеспечения делимости без остатка
формируемой разрешенной кодовой
комбинации на образующее число.
Идея
построения циклического кода (n,k)
сводится к тому, что информационную
часть кодовой комбинации G(x)
нужно преобразовать в комбинацию F(x),
которая без остатка делится на порождающий
полином Р(х) степени r=n-k.
Рассмотрим последовательность операций
построения циклического кода:
1.
Представляем информационную часть
кодовой комбинации в виде полинома
G(x).
Например информационная часть 110101.
Тогда
![]() .
.
2.
Умножаем G(x)
на одночлен
![]() ( старшую степень порождающего полинома
( старшую степень порождающего полинома
Р(х) ) и получаем![]() .
.
Пусть
у нас порождающий полином 1011![]() ,
,
тогда
![]() .
.
3. Делим
![]() на
на
порождающий полином Р(х), при этом
получаем остаток от деленияR(x).
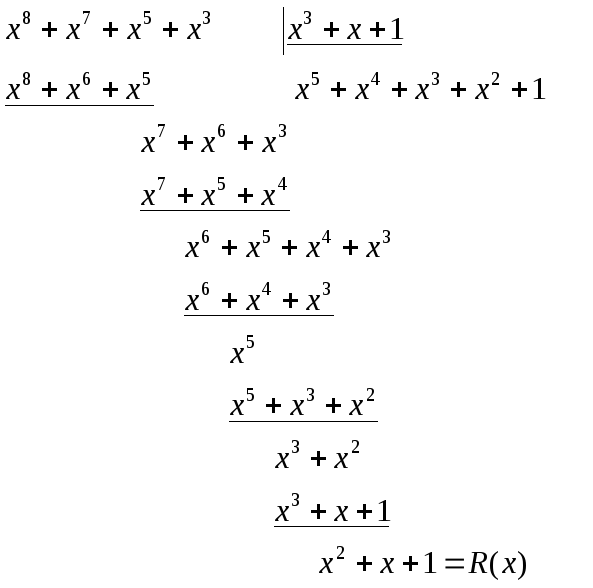
Добавим
полученный остаток R
(x)
к комбинации
![]() и
и
получим комбинацию![]() ,
,
которая будет передана в линию. Данная
комбинацияF(x)
делится без остатка на образующий
полином и представляет собой разрешенную
кодовую комбинацию циклического (n,k)
кода. На приеме производится деление
полученной кодовой комбинации на
образующий полином. Если ошибок нет, то
деление пройдет без остатка. Если при
делении получен остаток, то комбинация
принята с ошибками.
При
использовании в циклических кодах
декодирования с исправлением ошибок
остаток от деления может играть роль
синдрома. Нулевой синдром указывает на
то, что принятая комбинация является
разрешенной. Всякому ненулевому синдрому
соответствует определенная конфигурация
ошибок, которая и исправляется.
Построение
кодеров, декодеров.
Пример:
Кодер
строится на основе полинома P(x).
![]()
=> 1011
–
веса
При
построении устройства число ячеек
регистров сдвига берется по высшей
степени образующего полинома
![]() =>
=>
3 регистра сдвига; число регистров
задержки берется также по высшей степени
образующего полинома; число сумматоров
по модулю два берется по весовой части
образующего полинома минус единица =>
3-1=2m.
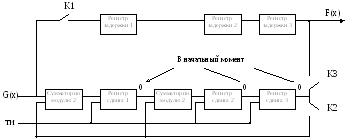
Состояния
регистров (1,2,3
– регистры; m
– сумматоры)
На
вход подается
![]() 110101000
110101000

Декодер
–
правила построения такие же, как у
кодера, но количество регистров задержки
определяется по высшей степени
информационной комбинации плюс 1
5+1=6

Деление
на образующий полином происходит за 9
тактов. Пока идет деление на образующий
полином К2 разомкнут, а К1 замкнут в
течении 6 тактов пока идет запись
информационных импульсов. После 6 такта
К1 размыкается. После 10 такта К2 замыкается
и формируется сигнал:
1. Если хотя бы в
одной ячейке регистра будет «1», то
значит произошла ошибка. Формируется
сигнал «1» и информация из регистров
сдвигов будет удаляться.
2. Если во всех
ячейках регистров сдвига будут «0», то
формируется сигнал «0» и информация
будет выдана потребителю.
Состояния
регистров

Если хотя бы в одной
ячейке регистра будет «1», то значит
произошла ошибка.
Информация из
регистров сдвигов будет удаляться. Если
во всех ячейках регистров сдвига будут
«0», то формируется сигнал «0» и информация
будет выдана потребителю.
Выбор образующего
полинома.
В
теории циклических кодов показано, что
образующий полином представляет собой
произведение так называемых минимальных
многочленов (![]() ),
),
являющихся простыми сомножителями,
(т.е. делящимися без остатка лишь на себя
и на 1).
Кроме
образующего полинома необходимо найти
и количество проверочных разрядовr.
![]() =1
=1
если n=7,
то
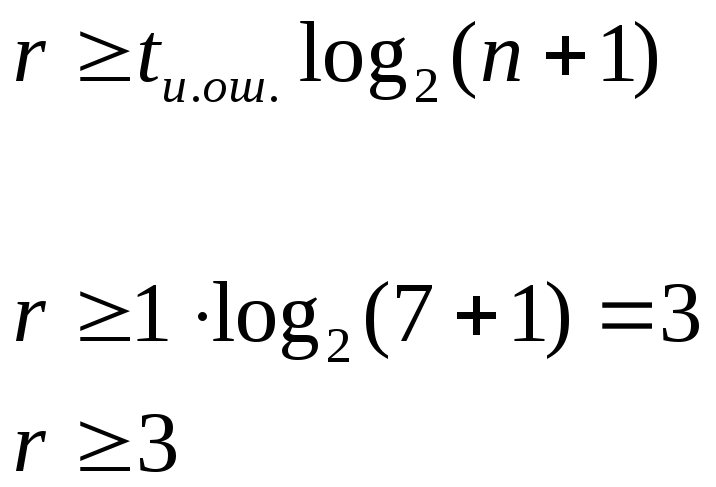
tи.ош
– число ошибок, исправляемых циклическим
кодом.
После
определения количества проверочных
разрядовr
вычисление образующего полинома удобно
осуществить, пользуясь таблицей
минимальных многочленов.
Ниже приведена часть такой таблицы.
r | Pr(x) | Двоичная |
2 |
| 111 |
3 |
| 1011 1101 |
В частности, если
r=3,
tи.ош=1,
j=2*1-1=1,
образующий полином будет представлять
собой единственный минимальный многочлен
P(x)= x3+x+1
(первая строка, второй столбец таблицы
). Соответственно образующее число равно
1011.
Синдром циклического
кода.
Синдром циклического
кода определяется суммой по модулю 2
принятых проверочных элементов и
элементов проверочной группы,
сформированных из принятых элементов
информационной группы. В циклическом
коде для определения синдрома следует
разделить принятую кодовую комбинацию
на кодовую комбинацию порождающего
полинома. Если все элементы приняты без
ошибок, то остаток от деления R(х)
равен нулю. Если есть ошибки, то остаток
не будет равен нулю. Следовательно,
синдромом циклического кода является
многочлен R(x).
Обнаружение и исправление ошибок
производится только на основе анализа
синдрома. В зависимости от остатка
определяется элемент в котором произошла
ошибка. Для исправления ошибок необходимо
чтобы количество ненулевых остатков
равнялось количеству элементов n
( при исправлении одной ошибки ) или
числу комбинаций из n.
Соседние файлы в папке Будылдина2
- #
11.04.20152.54 Mб19ДКР рисунок Mumarev.vsd
- #
11.04.20152.49 Mб22ДКР рисунок.vsd
- #
- #
- #
- #
Источник
Выбор образующего полинома
При построении циклических кодов важную роль играют образующие полиномы, поскольку они полностью определяют корректирующие свойства кода.
Как мы уже отмечали остаток от деления КК циклического кода на образующий полином является синдромом этого кода. Для того, чтобы код мог исправлять ошибки, количество ненулевых остатков должно быть равно количеству комбинаций с различным сочетанием ошибок. Если код исправляет однократную ошибку, то число различных остатков равно количеству элементов в КК длиной «n». В общем случае число различных остатков должно быть равно Сntи. Поэтому в качестве образующих полиномов берутся многочлены из класса непроводимых.
Непроводимыми называются такие полиномы, которые делятся без остатка только на 1 и сами на себя.
Кроме того, среди непроводимых полиномов, отбирают так называемые примитивные.
Примитивным считается полином степени r, если он обеспечивает максимальное число непроводимых полиномов той же степени r. Таких остатков должно быть не менее 2r-1/
Примитивные полиномы выбираются из специальных таблиц.
МККТТ рекомендует V.41 – P(x)= x16+x12+ x5+1 — «Аккорд 1200»
В циклических кодах синдром (остаток) является опознавателем ошибки, но не указывает непосредственно на место ошибки в принятой КК.
Идея исправления ошибок базируется на том, что ошибочная комбинация после определенного числа циклических сдвигов «подгоняется» под полученный остаток таким образом, что в сумме с остатком она дает исправленную комбинацию.
Остаток при этом представляет собой разницу между искаженным и исправленным разрядами. Единицы в остатке стоят на местах искаженных разрядов в «подогнанной» циклическими сдвигами КК.
Циклически сдвигают искаженную КК до тех пор, пока число единиц в остатке не будет равно числу ошибок, которые может исправлять данный код.
При этом место ошибки не имеет значения. В этом смысле циклические коды могут исправлять пачки ошибок, если длина пачки ошибок не превышает кратность исправляемых ошибок tu
Алгоритм оптимального декодирования на основе анализа веса
1. Принятая КК делится на образующий полином
2. Если остаток нулевой, то КК выдается получателю. Если не нулевой, то выполняют п.3
3. Подсчитывается вес остатка; если w≤ tu , то принятая КК складывается по модулю 2 с полученным остатком, если w> tu ,то выполняется п.4
4. Производим циклический сдвиг КК влево на один разряд. Делим полученную в результате сдвига КК на образующий полином. Если вес остатка w≤ tu, то складываем остаток с КК и полученную КК сдвигаем вправо на один разряд – будет исправленная КК. Если w> tu, то выполняется п.5
5. Повторяем п.4 до тех пор, пока не будет w≤ tu. КК, полученная в результате последнего циклического сдвига влево, суммируется с последним остатком. Далее выполняется п.6
6. Производится циклический сдвиг вправо на столько разрядов, на сколько была сдвинута исходная КК относительно принятой КК. В результате получим исправленную КК.
Рассмотрим пример
Пусть передаем КК 1001110 кода (7,4), образующий полином Р(х)=1011 (х3+х+1). Пусть в принятой КК искажен 4 разряд. d0=3, т.е. код исправляет однократную ошибку tu=1, т.е. приняли мы КК →1000110. Попытаемся обнаружить и исправить эту ошибку
1. Делим принятую КК на Р(х):
1000110 1011
1011 101
1111
1000
1011
Получим остаток 11, его вес равен 2> tu=1
2. Производим сдвиг полученной КК влево на 1 разряд
1000110→0001101
делим на Р(х)
0001101 1011
1011
110 — вес остатка 2> tu=1
3. Еще сдвигаем влево КК
0001101→0011010 делим на Р(х)
0011010
1011 1011
1100
111 — вес остатка 3> tu=1
4. Еще сдвигаем влево КК
0011010→0110100 делим на Р(х)
0110100 1011
1011
1100
1011
1110
101 — вес остатка 2> tu=1
5. Еще сдвигаем влево КК
0110100→1101000, делим на Р(х)
1101000 1011
1011
1100
1011
1110
1011
1010
1011
1 — вес остатка w= tu =1
6. Складываем последнее делимое с остатком
1101000
1101001
7. Сдвинем эту КК вправо на 4 разряда, т.к. мы сдвигаем исходную КК влево на 4 разряда:
1101001 →1110100
1110100 →0111010
0111010 →0011101
0011101 →1001110
Получим исправленную КК – сравним с переданной: 1001110
Источник
